简介#

Link-Cut Tree 是一种用来解决动态树问题的数据结构。

Splay 是 LCT 的基础，请保证您已经掌握了 Splay。

动态树问题#

维护一个森林，支持删除某条边，加入某条边，并保证加边，删边之后仍是森林。我们要维护这个森林的一些信息。

一般的操作有两点连通性，两点路径权值和，连接两点和切断某条边、修改信息等。

实链剖分#

首先回顾重链剖分，我们按照子树大小进行剖分，并重新为节点标号。

我们发现树被划分成了许多以链为单位的子段，使用线段树进行维护。

那么我们想到可以自己选定边用以剖分，创造一种新的剖分来解决动态树问题。

定义实链剖分#

对于一个点，我们可以选择一条出边进行剖分，我们称被选择的边为实边，其他边则为虚边。

对于实边，我们称它所连接的儿子为实儿子。对于一条由实边组成的链，我们同样称之为实链。

由于剖分的边是我们选择的，灵活且可变。正是它的这种灵活可变性，我们采用 Splay 来维护这些实链。

辅助树#

一棵辅助树由一些 Splay 构成，每棵辅助树维护的是原森林中的一棵树，一些辅助树构成了 LCT，其维护的是整个森林。

辅助树由多棵 Splay 组成，每棵 Splay 维护原树中的一条实链，且这棵 Splay 的中序遍历与原实链顺序相同。
原树每个节点与辅助树的 Splay 节点一一对应，且每条实链对应一棵 Splay。
辅助树的各棵 Splay 之间并不是独立的。每棵 Splay 的根节点的父亲节点指向原树中这条链的父亲节点。这条边与 Splay 中通常的父子关系区别在于儿子认父亲，而父亲不认儿子，对应原树的一条虚边。

由于辅助树的性质，我们维护任何操作都不需要维护原树，只需要维护辅助树即可。

辅助树是可以在满足辅助树、Splay 的性质下任意换根的。虚实链变换也可以轻松在辅助树上完成，这就实现了动态维护树链剖分。

实现#

需要用到的数组#

son[x][0/1] 左右儿子。
fa[x] 父亲。
val[x] 点权。
tag[x] 翻转标记。
题目需要用到的其他数组。

需要用到的函数#

IsRoot(x) 判断 $x$ 是否为当前 Splay 的根。
Reverse(x) 翻转 $x$ 的子树。
PushUp(x) 向上更新数据。
PushDown(x) 向下传递标记。
Update(x) 从当前 Splay 的根下传标记到 $x$ 。
Get(x) 获取 $x$ 是 Splay 中父亲的那个儿子。
Rotate(x) 将 $x$ 向上旋转一层。
Splay(x) 伸展 $x$ 到当前 Splay 的根。
Access(x) 将当前原树的根到 $x$ 拉成一条实链。
MakeRoot(x) 将 $x$ 换成当前原树的根。
FindRoot(x) 返回 $x$ 所在原树的根节点编号。
Split(x,y) 提取出 $x,y$ 间的路径。
Link(x,y) 在 $x,y$ 之间连一条边。
Cut(x,y) 断开 $x,y$ 之间的边。
题目需要用到的其他函数。

宏定义#

lson(x) 表示 son[x][0]。
rson(x) 表示 son[x][1]。

IsRoot(x)#

#define IsRoot(x) (lson(fa[x])!=x&&rson(fa[x])!=x)
//如果 x 不是父亲的左儿子也不是右儿子，就一定是 Splay 的根

Reverse(x)#

#define Reverse(x) swap(lson(x),rson(x)),tag[x]^=1

PushUp(x)#

void PushUp(int x) {
    //更新题目要求的内容
}

PushDown(x)#

void PushDown(int x) {
    if(tag[x]) {
        if(lson(x)) Reverse(lson(x));
        if(rson(x)) Reverse(rson(x));
        tag[x]=0;
    }
    //下传题目要求的其它标记
}

Update(x)#

void Update(int x) {
    if(!IsRoot(x)) Update(fa[x]);
    PushDown(x);
}

Get(x) & Rotate(x) & Splay(x)#

Splay 的函数，有一些改变。

#define Get(x) (son[fa[x]][1]==x)
void Rotate(int x) {
    int y=fa[x],z=fa[y],k=Get(x);
    if(!IsRoot(y)) son[z][Get(y)]=x;
    //如果 y 是根，那么 y 和 z 之间的边是虚边，z 不连儿子
    son[y][k]=son[x][!k],fa[son[x][!k]]=y;
    son[x][!k]=y,fa[y]=x,fa[x]=z;
    PushUp(y),PushUp(x);
}
void Splay(int x) {
    Update(x);//在 Splay 之前要把旋转会经过的路径上的点都 PushDown
    while(!IsRoot(x)) {
        int y=fa[x];
        if(!IsRoot(y)) Rotate(Get(y)==Get(x)?y:x);
        Rotate(x);
    }
}

Access(x)#

伸展 $x$ 到 Splay 的根。
将 $x$ 的右儿子（因为左儿子比 $x$ 浅，右儿子比 $x$ 深）修改为上一个 $x$ ，如果是第一次就改为空。
更新 $x$ 的信息。
将 $x$ 变为 $x$ 的父亲，重复以上操作。

比如这样一棵树：

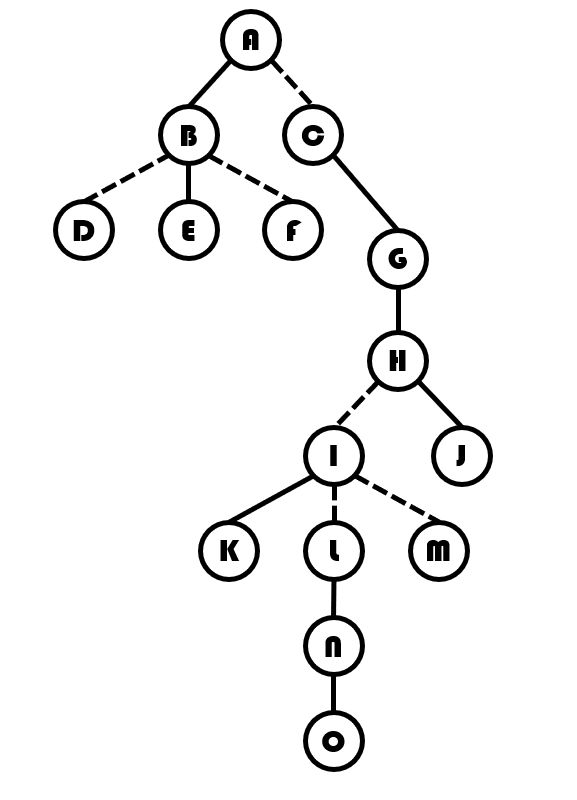
我们现在要将它的根 $A$ 到 $N$ 拉成一条实链。如图：

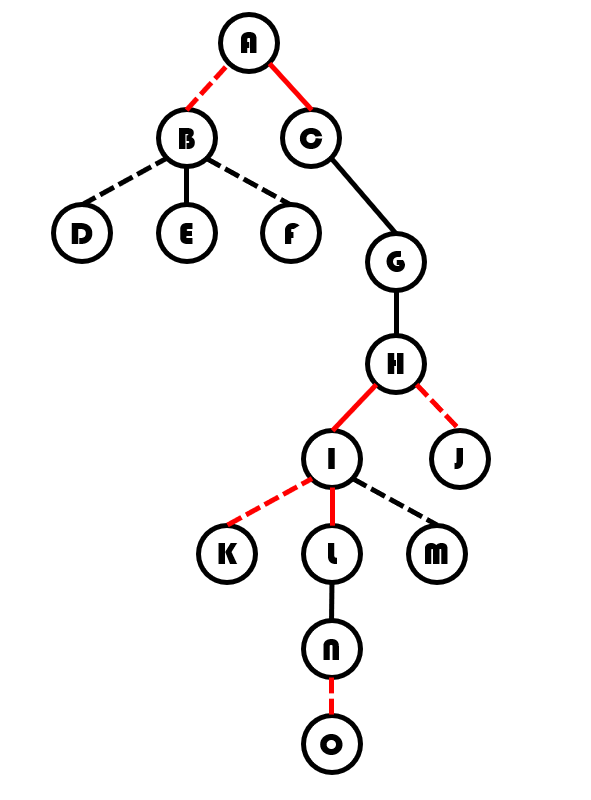
它的辅助树也许是这样的：

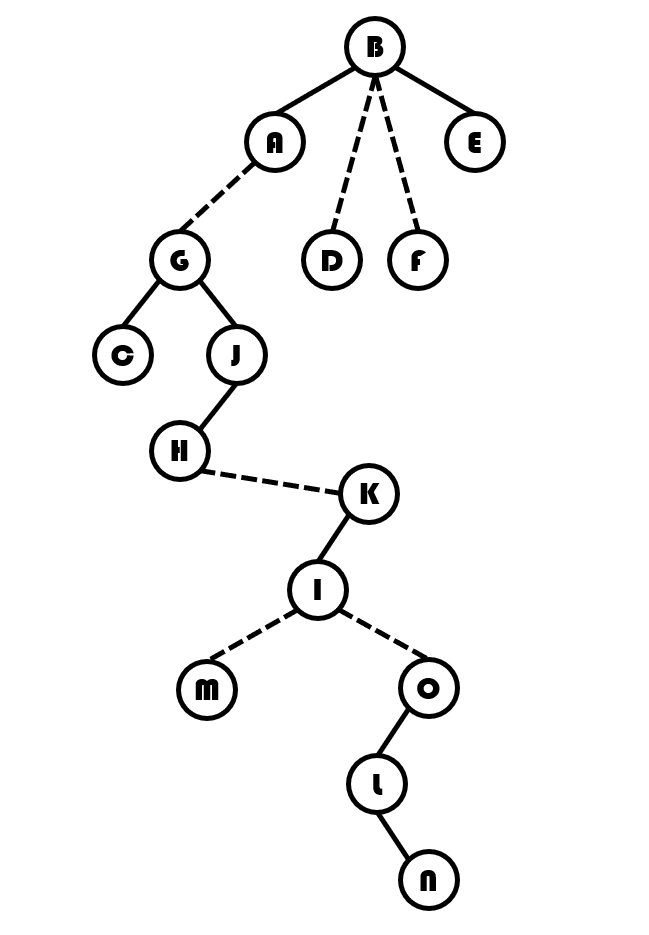
我们将每一个 Splay 圈起来。如图：

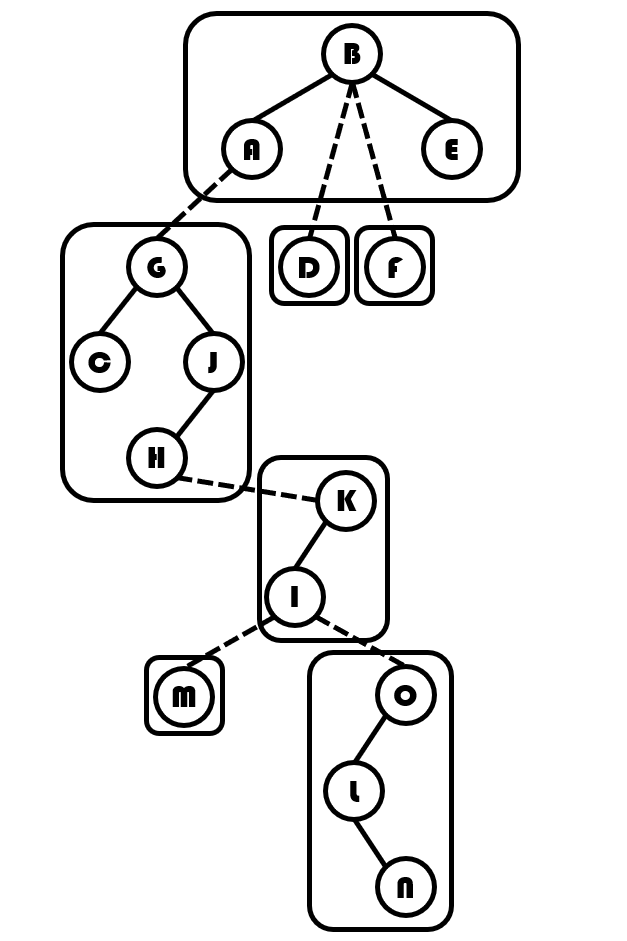
那么我们按上面的步骤拉成一条实链，就像这样：

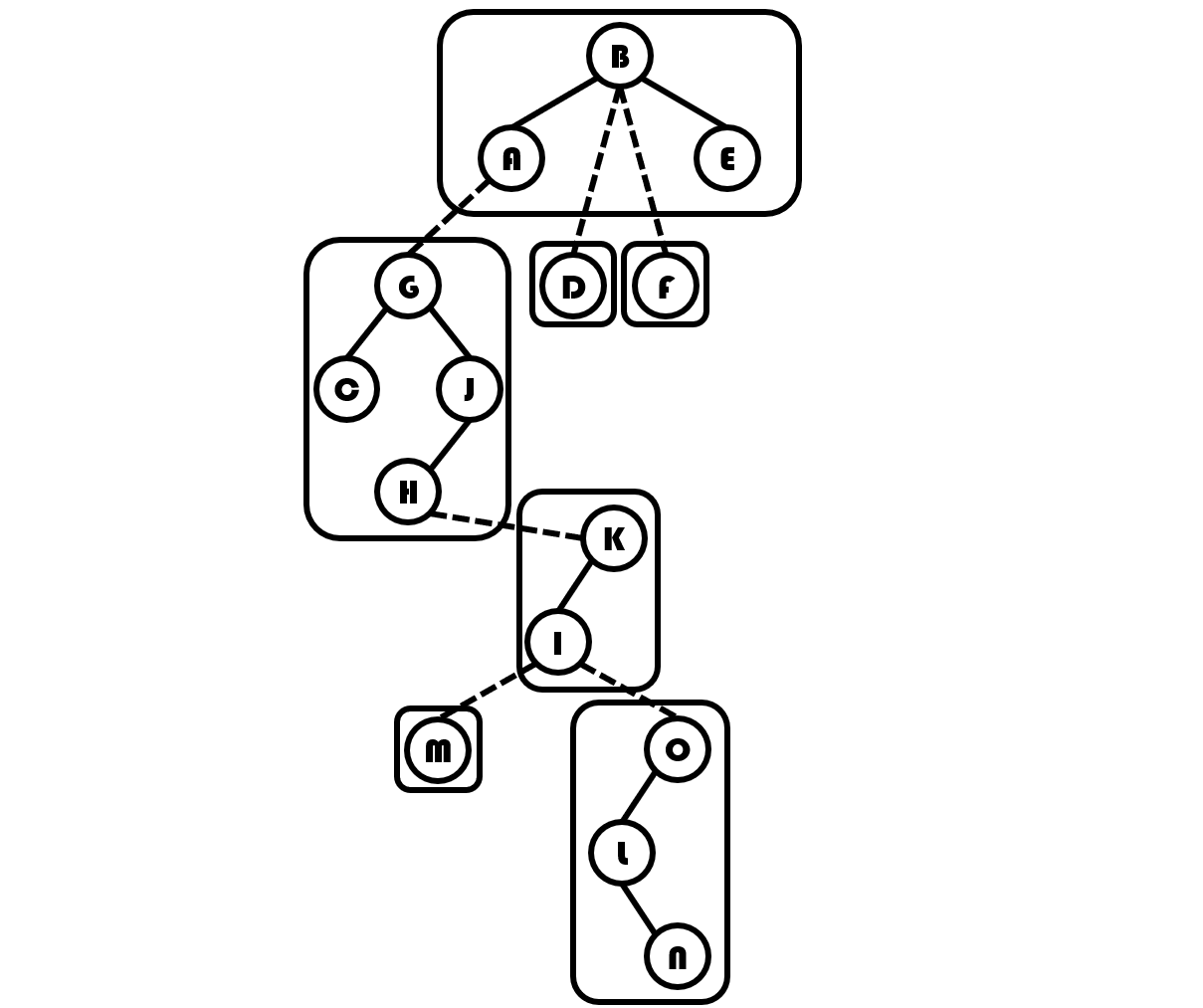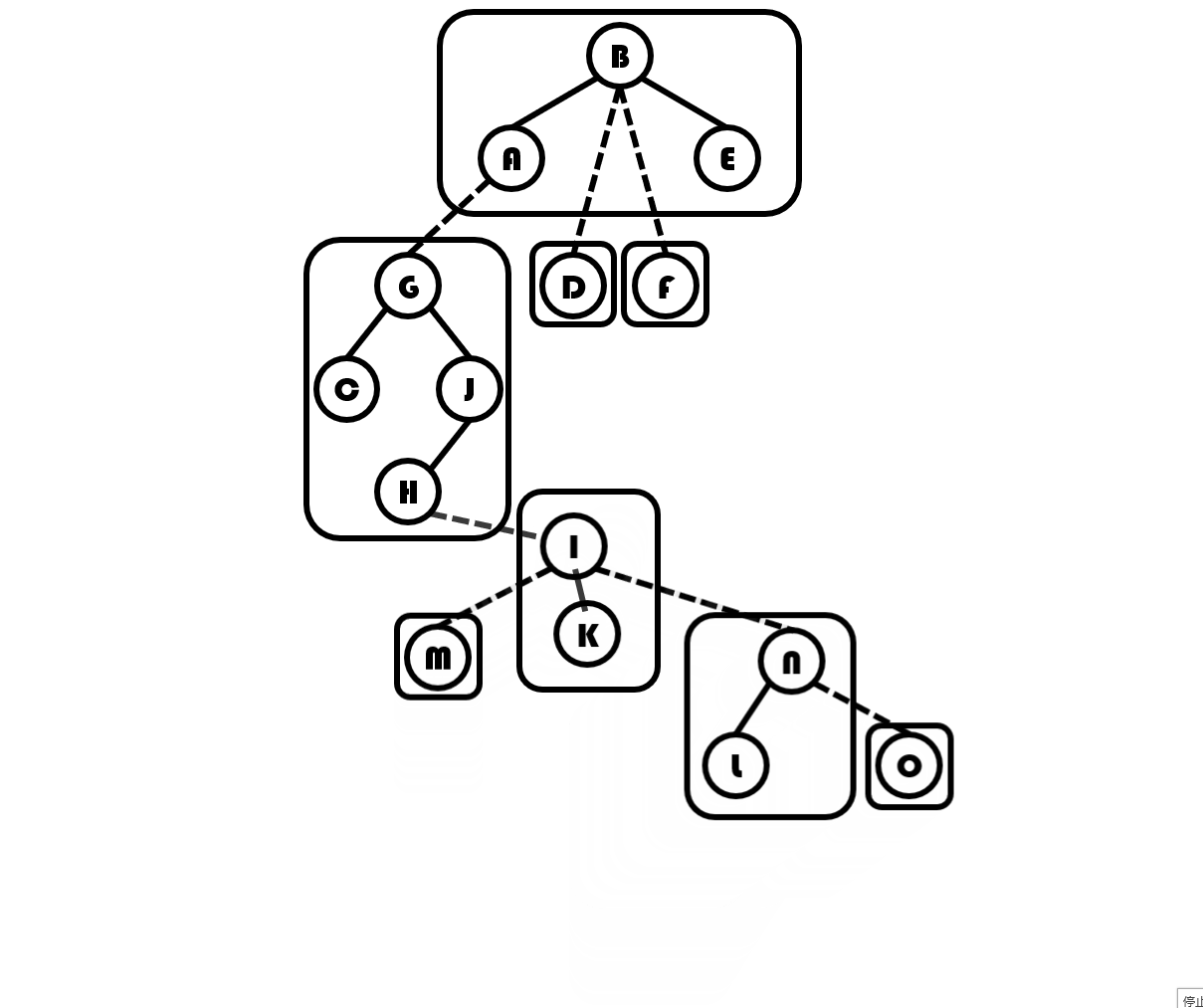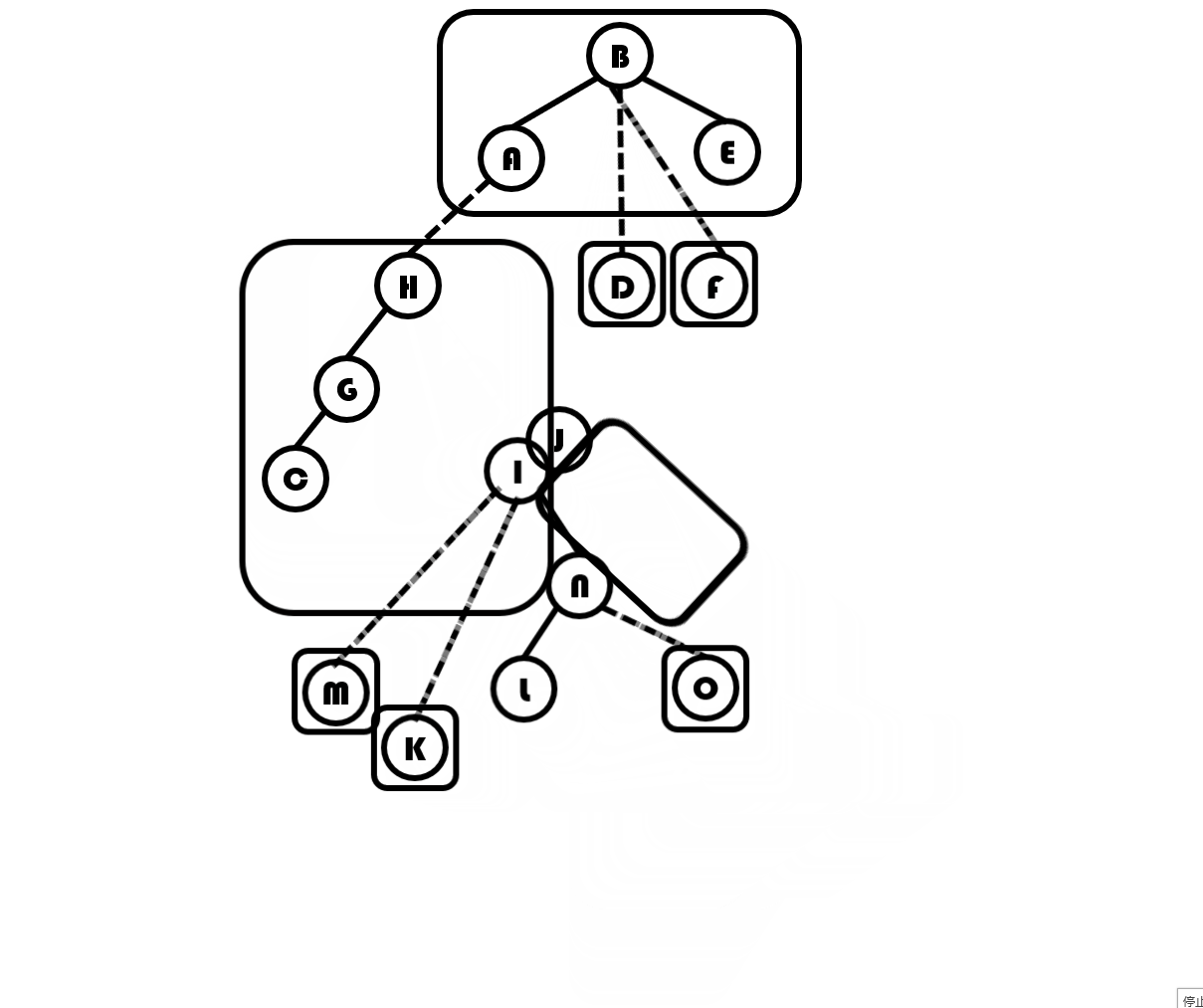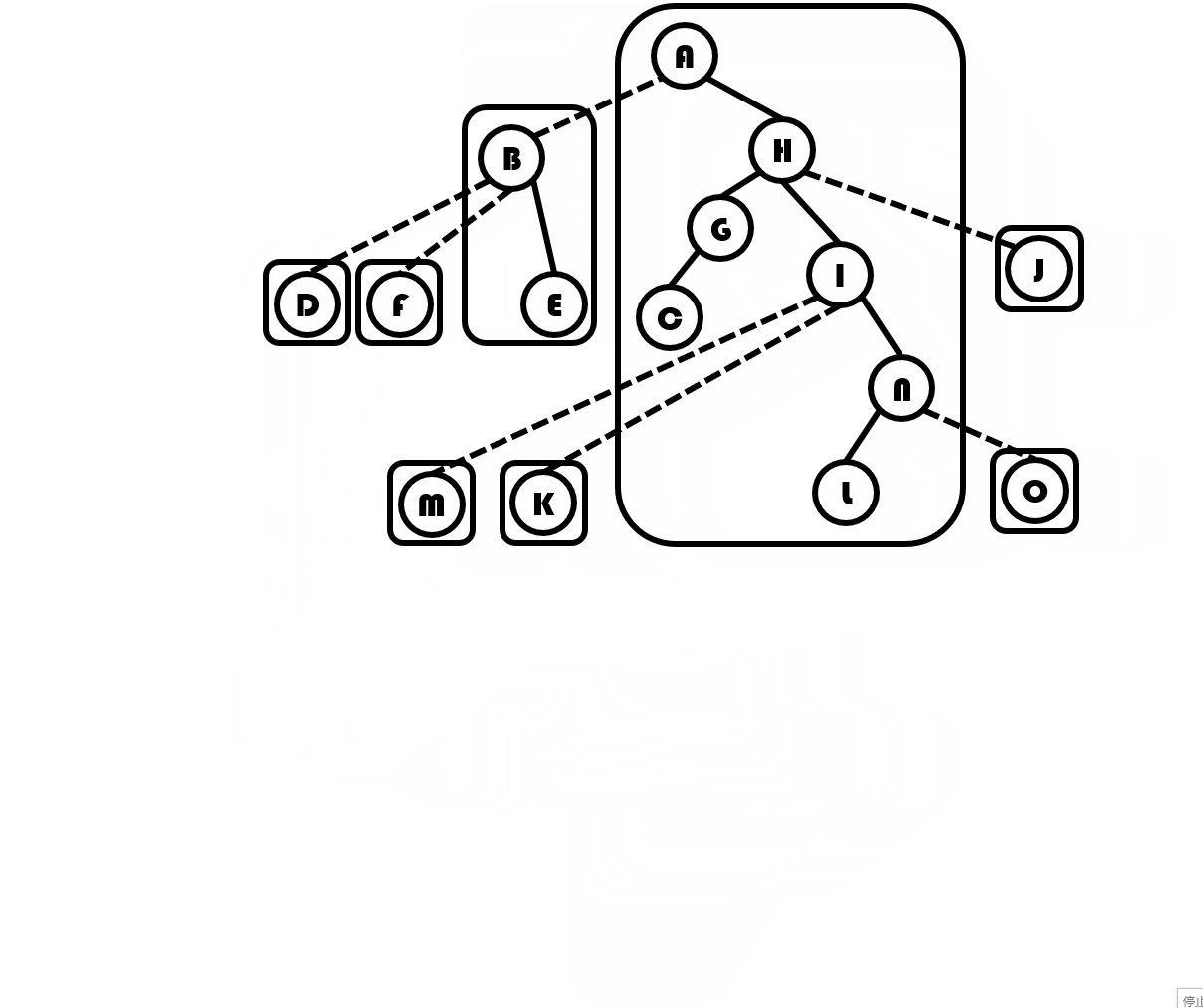
最后辅助树会变成这样：

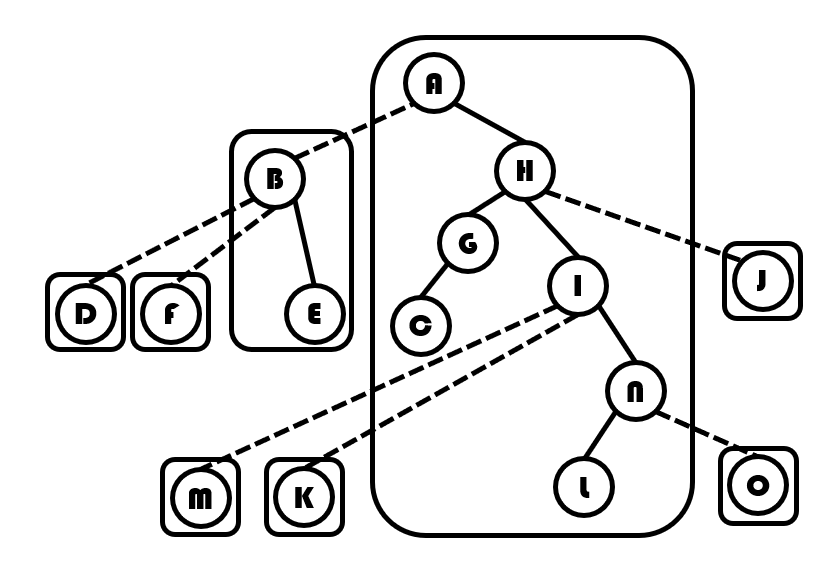
中序遍历 $N$ 所在的 Splay 可以得到 $ACGHILN$ ，与原树相同。

void Access(int x) {
    for(int y=0;x;y=x,x=fa[x])//y 为上一次的 x
        Splay(x),rson(x)=y,PushUp(x);
}

MakeRoot(x)#

只是把根到某个节点的路径拉起来并不能满足我们的需要。

更多时候，我们要获取指定两个节点之间的路径信息。

然而可能这两个点不是祖孙关系，即该路径不能满足按深度严格递增的要求。

由于 Splay 维护一条链，这样的路径不能出现在一个 Splay 中。

考虑将树用有向图表示出来，给每条边定一个方向，表示从父亲到儿子的方向。容易发现换根相当于将 $x$ 到根的路径的所有边反向。

如这棵树：

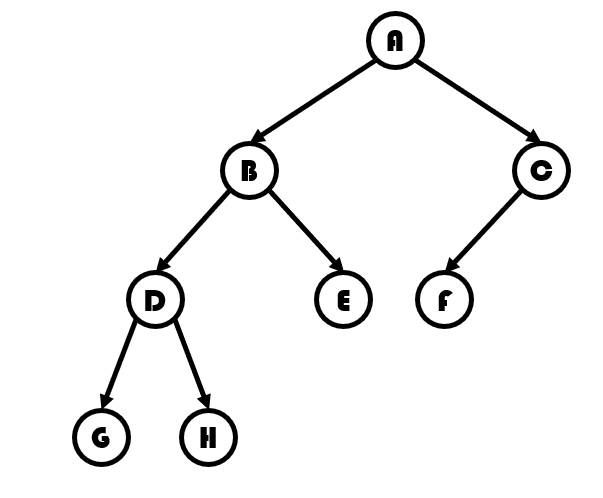
以 $D$ 为根后变成了这样，就是将 $A$ 到 $D$ 的路径反向。

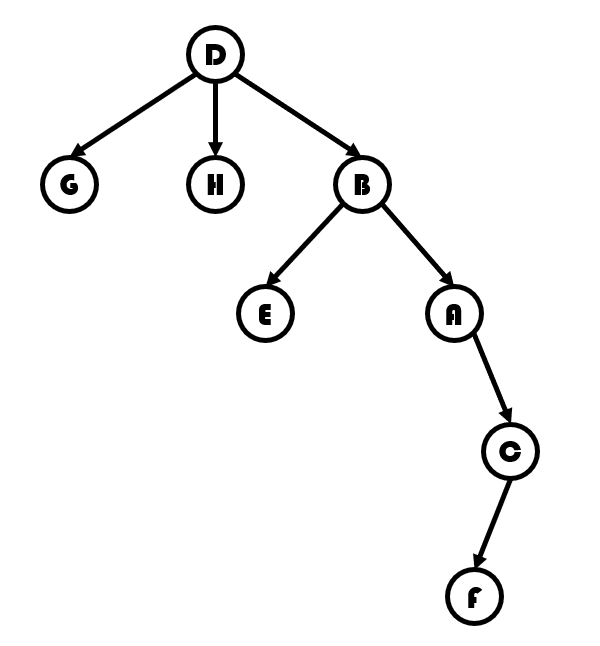
因此先将 $x$ 到根的路径分离，再将其翻转即可。

void MakeRoot(int x) {
    Access(x);
    Splay(x);//将 x 伸展到根
    Reverse(x);//翻转整棵 Splay
}

FindRoot(x)#

先 Access(x)，再 Splay(x)。

由于根是树里深度最小的那个，所以就一直往左儿子走，沿途 PushDown 即可。

每次查询之后需要把查询到的答案对应的节点伸展到根以保证复杂度。

int FindRoot(int x) {
    Access(x);
    Splay(x);
    while(lson(x)) {//一直往左走
        PushDown(x);
        x=lson(x);
    }
    Splay(x);
    return x;
}

Split(x,y)#

先 MakeRoot(x)，然后 Access(y)，再 Splay(y)。

这样从 $x$ 到 $y$ 的路径就被放在一棵 Splay 里了，而且 $y$ 是这棵 Splay 的根。

void Split(int x,int y) {
    MakeRoot(x);
    Access(y);
    Splay(y);
}

Link(x,y)#

连接两个点其实很简单，先 MakeRoot(x)，然后把 $x$ 的父亲指向 $y$ 即可。

显然，这个操作肯定不能发生在同一棵树内，所以记得先判一下 $y$ 的根是否为 $x$ 。

void Link(int x,int y) {
    MakeRoot(x);
    if(FindRoot(y)==x) return;//数据保证合法可以省略
    fa[x]=y;
}

Cut(x,y)#

如果数据保证合法，那么直接 Split(x,y)，此时 Splay 中只有 $x,y$ 两个节点，且 $y$ 为 Splay 的根， $x$ 在原树的深度比 $y$ 浅，那么只要把 $y$ 的左儿子和 $x$ 的父亲制成 $0$ 即可。

如果数据不保证合法，那就先 MakeRoot(x)，还需要判断一下 $x,y$ 之间是否有边。当 $x,y$ 在同一棵 Splay 里且 $x$ 为 Splay 的根时，这需要满足三个条件：

$x,y$ 连通。
$y$ 的父亲为 $x$ 。
$y$ 没有左儿子，因为 $y$ 的左儿子在 $x,y$ 的路径上。

void Cut(int x,int y) {
    MakeRoot(x);
    if(FindRoot(y)!=x||fa[y]!=x||lson(y)) return;
    //FindRoot 里面已经 Access 过了，且把 x 伸展到了根
    fa[y]=rson(x)=0;//x 是根，深度比 y 浅，所以是右儿子
    PushUp(x);
}